Learning Hierarchical Features from Generative Models

TLDR: Current ways of stacking variational autoencoders on top of each other may not always provide a hierachy of meaningful features. In fact, we showed in a recent ICML paper that while existing approaches have shortcomings, a new ladder architecture can often learn distentangled features.

Variational Autoencoders (or VAE in short) (Kingma and Welling 2014) are one of the most popular class of deep generative models. They define a probability distribution $p(x \lvert z)$ (often parameterized by a neural network) that generates data $x$ given some latent variables $z$, which are sampled from a simple prior (Gaussian). The goal is often to learn a model where $z$ capture latent factors of variation in the data, corresponding to “features” that can be used for semi-supervised learning (Kingma et al. 2014).

Deeper is Not Always Better for Hierarchical VAEs

Several researchers (Kingma and Welling 2014; Rezende, Mohamed, and Wierstra 2014; Sønderby et al. 2016) have proposed “hierarchical VAEs”,

\[p(x \lvert z) = p(x|z_1)\prod_{\ell = 1}^{L-1} p(z_\ell | z_{\ell+1})\]

where VAEs are effectively stacked on top of each other:

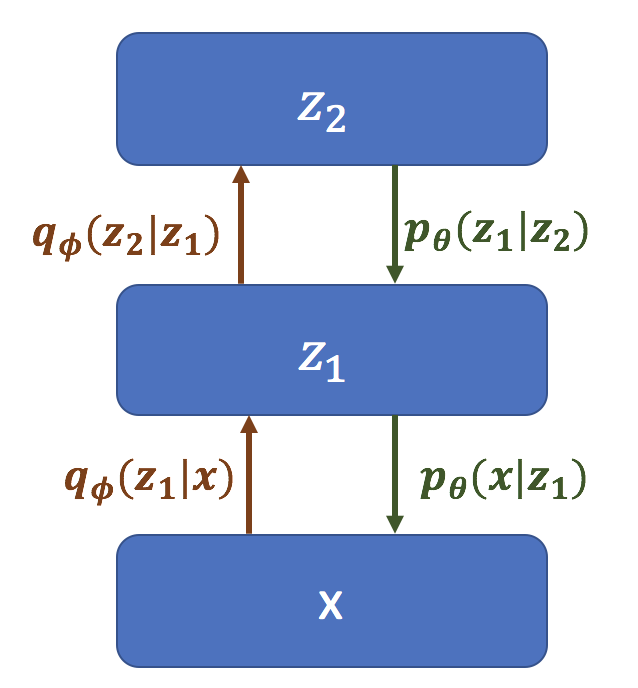
Graphical model for a Hierarchical VAE.

There are two potential advantages of using hierarchical VAEs:

They could improve the so-called Evidence Lower Bound (ELBO) (used as a proxy for the intractable log-marginal likelihood during learning) and decrease reconstruction error.
The stack of latent variables $z_\ell$ might learn a “feature hierarchy” similar to those learned by convolutional neural networks.

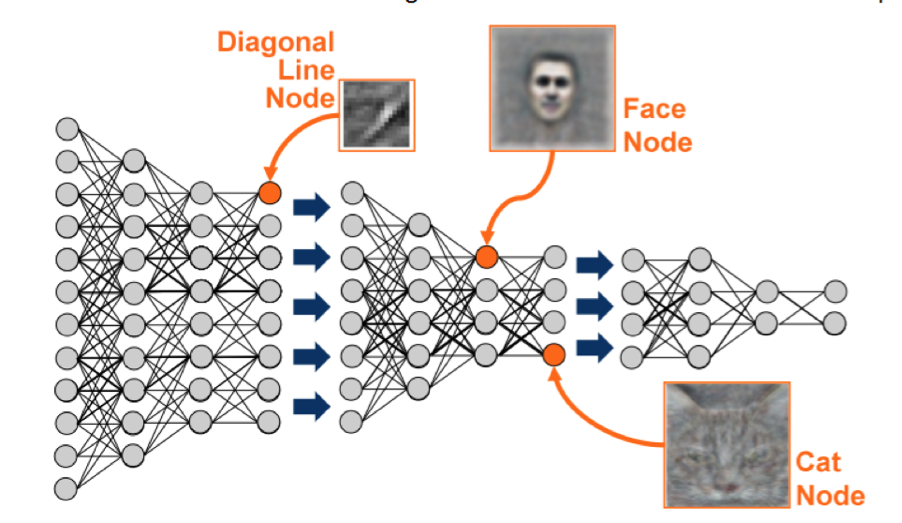
Convolutional Neural Nets are good at learning hierarchical features.

The first advantage has been validated by many recent works — hierarchical VAEs indeed seem to improve ELBO bounds ¹. The second argument, however, has not been clearly demonstrated ². In fact, it is difficult to learn a meaningful hierarchy when there are many layers of latent variables, and some consider this to be an inference problem (Sønderby et al. 2016).

We show in our recent ICML paper, Learning Hierarchical Features from Generative Models, that if the purpose is to learn structured, hierarchical features, using a hierarchical VAE has limitations. This is because under ideal conditions, layers above the first one are redundant.

To see this, let us assume that we already have a perfect generative model $p$ and its corresponding inference model $q$ that performs perfect posterior inference at every layer, such that at the first layer $p(z_1 \vert x) = q(z_1 \vert x)$. Then we can sample from the data distribution by the following Markov chain (assuming that the chain mixes):

\[x^{(0)} \sim p_{\mathrm{data}}(x), \quad z_1^{(0)} \sim q(z_1\vert x^{(0)}) \\ x^{(i)} \sim p(x\vert z_1^{(i-1)}), \quad z_1^{(i)} \sim q(z_1\vert x^{(i)}) \quad \forall i \in \{1, 2, \ldots \}\]

Note that if $q(z_1\vert x) = p(z_1\vert x)$, the above is just a Gibbs sampling chain for $p(x, z_1)$.

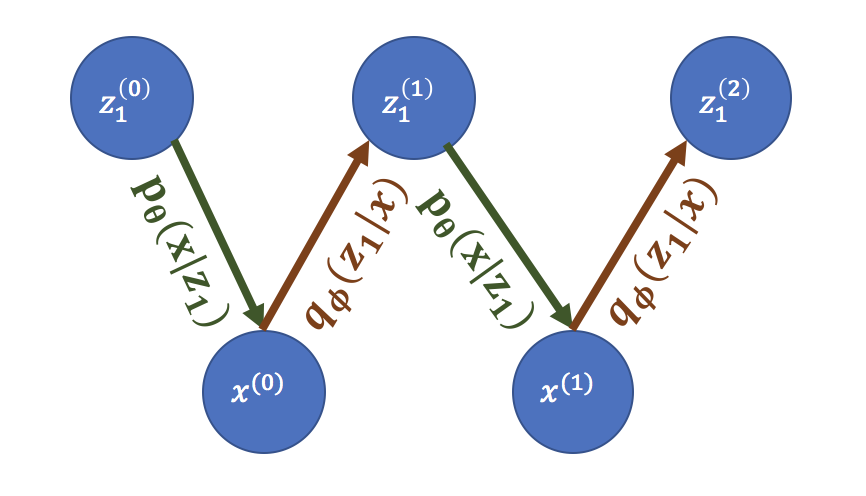
Generating the data distribution from a Gibbs sampling chain.

Therefore, it is difficult for hierarchical VAEs to learn features since the first layer contains all the information it needs to generate the data.

A Simple yet Effective Method for Learning Hierarchical Features

Instead of stacking VAEs on top of each other, we propose an alternative approach to introducing a hierarchy, which we call the Variational Ladder Autoencoder (VLAE) ³.

The basic idea is simple: If there is a hierarchy of features, some complex and some simple, they should be expressed by neural networks of differing capacities. Hence, we should use shallow networks to express low-level, simple features and deep networks to express high-level, complex features. One way to do this is to use an implicit generative model ⁴, where we inject Gaussian noise at different levels of the network, and use a deterministic mapping from the $z$ to $x$:

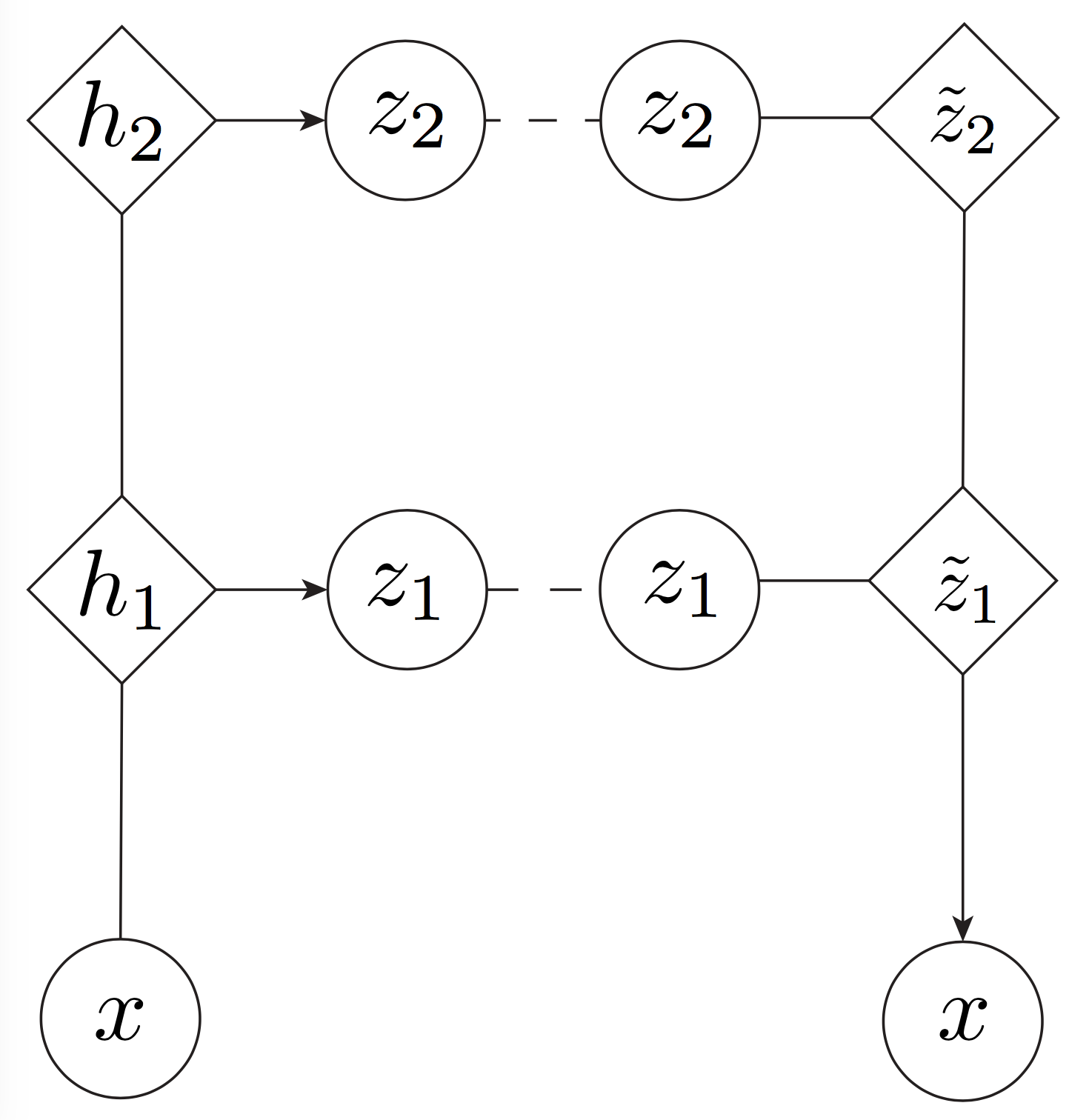
Graphical Diagram for VLAE. Here $h$ is deterministic activations for neural networks, while $z$ and $x$ are latent and observed variables respectively.

Training is essentially the same as for a single-layer VAE with $L_2$ reconstruction error. Below are some results from SVHN and CelebA: the VLAE models have 4 layers of $z$, and in each block we display the generated images when we change $z_\ell$ and fix the noise in all other layers $z_{\neg \ell}$ (from left to right, $z_1$ to $z_4$):

VLAE Generations for SVHN.

VLAE Generations for CelebA.

We observe that lower layers (left) learn simpler features, such as image color, while higher layers (right) learn more complex attributes, such as the overall structure. This demonstrates that a VLAE is able to learn hierarchical features, similar to what the InfoGAN (Chen et al. 2016) does.

The following is a comparison with the Hierarchical VAE model:

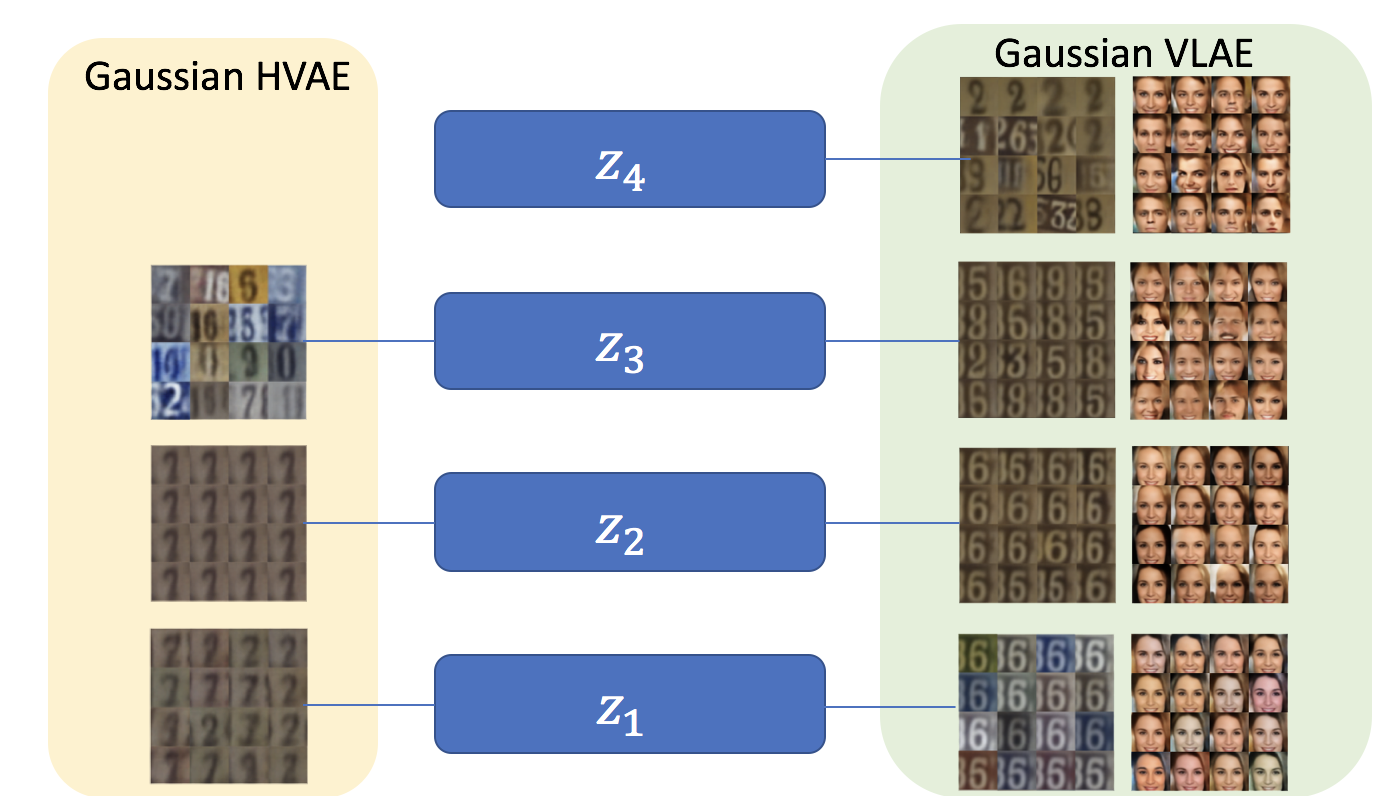
Comparison between HVAE and VLAE.

Code is available at: https://github.com/ermongroup/Variational-Ladder-Autoencoder.

Conclusion

In terms of learning hierarchical features, deeper is not always better for VAEs — however, by using a ladder architecture we can often learn structured features.

Footnotes

Though ELBO bounds and log-likelihood in general are not necessarily good measurements for generative models (Theis, Oord, and Bethge 2015). ↩
Except for in (Gulrajani et al. 2016), where a PixelCNN is used to model $p$. ↩
Coming up with a good name for this model was difficult with of all the existing work. ↩
(Tran, Ranganath, and Blei 2017) have also suggested a similar architecture, but our motivation is different (they focus on learning and inference with GANs, while we focus on learning hierarchical features). ↩

References

Kingma, Diederik P, and Max Welling. 2014. “Auto-Encoding Variational Bayes.” In International Conference on Learning Representations.
Kingma, Diederik P, Shakir Mohamed, Danilo Jimenez Rezende, and Max Welling. 2014. “Semi-Supervised Learning with Deep Generative Models.” In Advances in Neural Information Processing Systems, 3581–89.
Rezende, Danilo Jimenez, Shakir Mohamed, and Daan Wierstra. 2014. “Stochastic Backpropagation and Approximate Inference in Deep Generative Models.” ArXiv Preprint ArXiv:1401.4082.
Sønderby, Casper Kaae, Tapani Raiko, Lars Maaløe, Søren Kaae Sønderby, and Ole Winther. 2016. “Ladder Variational Autoencoders.” In Advances in Neural Information Processing Systems, 3738–46.
Chen, Xi, Yan Duan, Rein Houthooft, John Schulman, Ilya Sutskever, and Pieter Abbeel. 2016. “Infogan: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets.” In Advances in Neural Information Processing Systems, 2172–80.
Theis, Lucas, Aäron van den Oord, and Matthias Bethge. 2015. “A Note on the Evaluation of Generative Models.” ArXiv Preprint ArXiv:1511.01844.
Gulrajani, Ishaan, Kundan Kumar, Faruk Ahmed, Adrien Ali Taiga, Francesco Visin, David Vazquez, and Aaron Courville. 2016. “PixelVAE: A Latent Variable Model for Natural Images.” ArXiv Preprint ArXiv:1611.05013.
Tran, Dustin, Rajesh Ranganath, and David M Blei. 2017. “Deep and Hierarchical Implicit Models.” ArXiv Preprint ArXiv:1702.08896.

Ermon Group Blog

Home About