Decision Making with Uncertainty and Probabilistic Predictions

People constantly have to make decisions in face of uncertainty. For example, a patient might have to decide to undergo a treatment without knowing whether the treatment will work; a passenger might have to make travel plans without knowing whether flights will delay or not. How can machine learning help patients/passengers make decisions?

A running example we will use in this blog is a decision-maker we call Alice. She considers whether or not to take a flight for a conference. The flight ticket costs $100, the conference’s utility is $200, but Alice can only attend the conference if the flight arrives on-time. Therefore, if she takes the flight and the flight is on time, she gains $100 (i.e. $200 for the conference - $100 for the ticket); on the other hand, if the flight is delayed, she misses the conference and loses the $100 she paid for the ticket. If she doesn’t take the flight, she gains $0 in any case. Therefore, based on whether the flight will delay or not, taking the flight might be a good or bad decision for Alice.

To help Alice make decisions, the airline company can predict whether the flight will delay or not. The airline has a lot of data on past delays; based on the data, the airline can predict the probability of delay for a future flight with an algorithm such as decision tree or neural networks. As an example, for the flight Alice considers, the airline predicts that it delays with 30% probability.

If the predicted probabilities are correct, then each passenger could use them to make decisions. For example, Alice can compute her expected utility as

However, why should Alice believe in these probabilities? For example, the airline could just (intentionally) under-predict its delay probability to make its flight offerings more attractive. Even when the airline has no dishonest intent, predicting the future is difficult. To convey confidence about the predictions, an airline could claim that its predictions have a track record of being calibrated

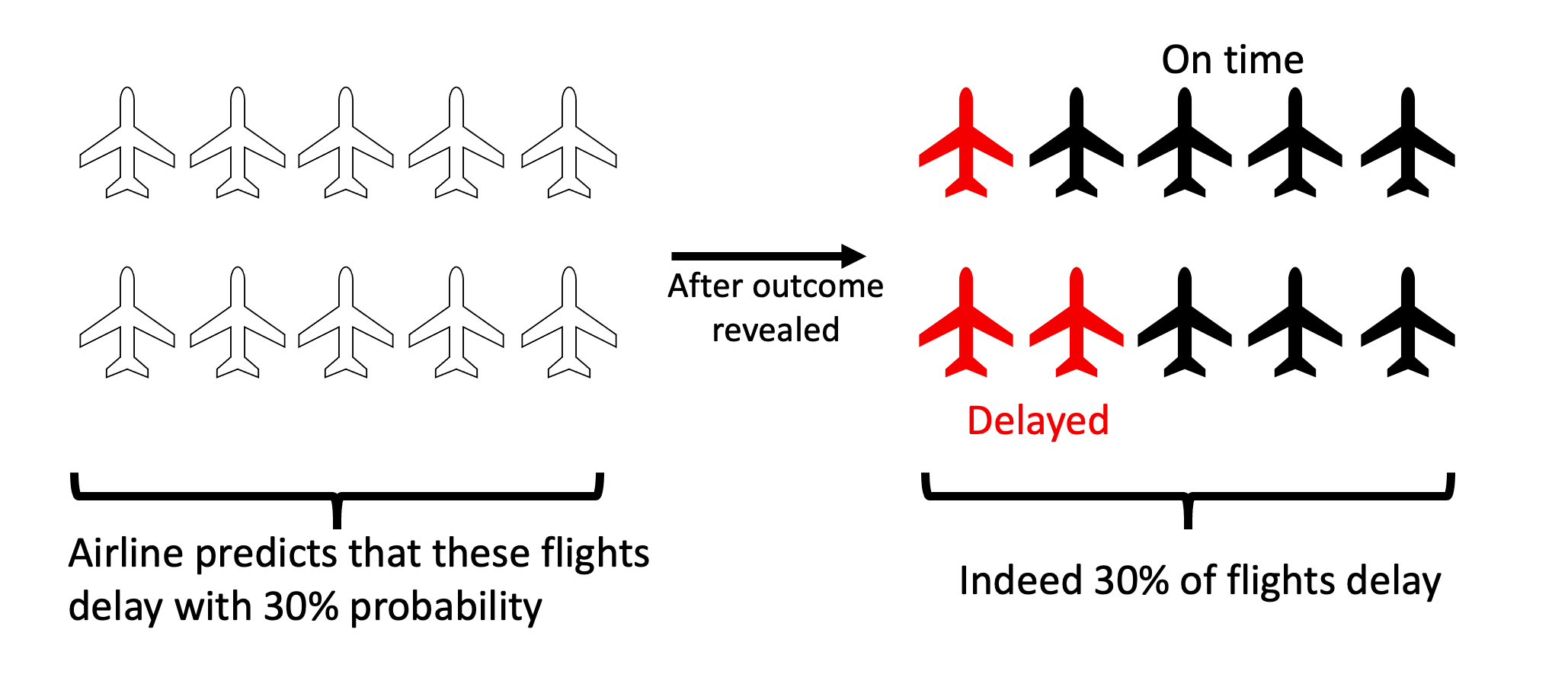
For example, as in the illustration above, the airline could claim: consider all flights for which I predicted would delay with 30% probability; among these flights, indeed 30% of the flights turned out delayed. At first sight, it might seem like Alice should believe in the 30% probability. However, consider the following situation

If Alice is a passenger from SFO, then actually 40% of flights delay. Even though the 30% probability is on average correct, it is correct neither for NYC nor SFO passengers. As other examples, the probabilities might be incorrect for flights in the morning or evening; rainy days or dry days; holiday seasons or regular seasons. Ultimately, the key problem is that each flight in unique, so the airline has never seen a completely identical flight to make claims about the past performance of that individual predictions. However, that individual prediction is the only thing that matters to Alice when she tries to decide whether to take the flight or not.

A Mechanism to Convey Confidence: An Example

In our paper we propose an insurance-like mechanism that 1) enables each decision-maker to confidently make decisions as if the advertised probabilities were individually correct, and 2) is implementable by the forecaster with provably vanishing costs in the long run.

We illustrate this mechanism by continuing Alice’s example above: Recall that the airline predicts a 30% chance of delay; if this probability were correct, Alice could compute her expected utility (which is $40).

However, Alice is not convinced that the 30% probability is correct. To reduce her risk, Alice proposes a bet (we will show how the bet is selected later): if the flight delays, the airline has to pay Alice $140; if the flight doesn’t delay, Alice pays the airline $60.

Alice’s perspective: If the airline agrees to bet with Alice, then if the flight delays, Alice’s total utility will be

if the flight doesn’t delay, Alice’s total utility will be

Therefore, whether the flight delays or not, Alice gains $40 from taking the flight. This is the same utility as if the predicted probability is correct. In other words, Alice can use the predicted 30% probability as if it is the true probability of delay when making decisions.

Airline’s perspective From the airline’s perspective, Alice’s bet is fair: under the the airline’s own predicted probability, the expected betting payout to Alice is $0:

In other words, if the airline genuinely believes in its own probability, the airline should agree to bet with Alice. By doing this, the Airline can give Alice full confidence in its predictions, which increases the attractiveness of its flight offerings.

In addition, we will see soon that the airline has nothing to lose: we will show that the airline has an prediction algorithm to guarantee that it doesn’t lose money from accepting such bets in the long run.

General Mechanism Definition and Its Benefits

We now generalize the numerical example above, and explain how this mechanism will work in general for any prediction and passenger utility

For each flight \(t\) the airline will predict some probability \(\mu_t \in [0, 1]\), and allow passengers to choose any bet that is “fair” as if \(\mu_t\) is the true probability. In other words, the passenger can choose any “stake” \(b \in \mathbb{R}\) and enter the following betting agreement with the airline: airline pays passenger \(b(1-\mu_t)\) if the flight delays, and passenger pays airline \(b\mu_t\) if the flight doesn’t delay. This is “fair” because

The passenger can also opt-out by choosing \(b=0\).

Why this mechanism benefits passengers In our paper (Proposition 2) we show that any passenger can have the same guarantee that Alice’s gets in our numerical example: he or she can always choose some $b \in \mathbb{R}$ such that

1. The choice of \(b\) only depends on information available to him or her (which is his/her own utilities, and the airline’s predicted probability \(\mu_t\))
2. His or her total utility (utility of flight + utility from betting) always equals the expected utility as if the predicted probability \(\mu_t\) is correct.

Why this mechanism doesn’t hurt airline (forecaster) In our paper (Theorem 1 and Corollary 1) we show that the airline (or forecaster) has nothing to lose: we design an online algorithm to make the predictions \(\mu_t, t=1, 2, \cdots, T\) such that when \(T\) is large the betting loss (for the airline) is guaranteed to vanish. The only requirement is that the maximum betting loss at each time step \(t\) is bounded, which the airline can easily enforce by limiting the maximum stake \(b\).

Our guarantee in Theorem 1 holds even when the passengers are adversarial. For example, if some malicious passenger Bob knows that the true probability of delay of a flight is actually 40% while the airline predicts it is 30%, Bob can choose some stake \(b\) to maximally profit from the airline’s mistake. Even though initially Bob could be successful, in the long run our online forecasting algorithm can adapt and prevent such exploitation.

From a very high level, our algorithm is based on the observation that the airline’s (forecaster’s) cumulative betting loss is upper bounded by a type of regret called swap regret (Blum and Mansour 2007); our prediction algorithm can modify any existing prediction algorithm to have vanishing swap regret (in the long run), so the betting loss also vanishes.

Why this mechanism benefits airline (forecaster) If we assume that some passengers are risk averse (the fundamental assumption of the insurance industry), then this mechanism can also benefit the airline. For example, Alice might be hesitant to buy the flight ticket because she doesn’t know whether the decision has positive utility or negative utility. If the airline can convey confidence and assure Alice that she can receive $40 utility if she takes the flight, Alice should be more willing to purchase the flight ticket. Consequently, the airline can also charge a higher ticket price without reducing sales. In our example above, with the betting mechanism Alice should be willing to pay up to $140 ticket price (at $140 her utility is guaranteed to be exactly zero), but without it she might not be willing to pay $100.

The airline can benefit from this mechanism even when only a small percentage of customers are risk averse, and the rest are risk neutral or even risk seeking. The bet is an option — each customer can choose to opt-out by selecting the stake \(b=0\). As one of our experiments in the paper, we run a simulation on real flight delay data and vary the proportion of risk averse passengers. By offering the opportunity to bet, we show that the airline can increase both its revenue and the overall utility (i.e. airline’s revenue + total passenger utility). Even when only 20% of passengers are risk averse, the airline’s revenue still increases by around 10%.

References

1. Blum, Avrim, and Yishay Mansour. 2007. “From External to Internal Regret.” Journal of Machine Learning Research 8 (6).